Lidt om rumakustik
Alle hi-fi entusiaster bør, hvis de ikke allerede ved det, vide lidt om rumakustik. Herunder hører hvorledes et rum kan dimensioneres for at opnå en akustik, der frembringer den bedst mulige lydgengivelse fra ens hi-fi anlæg. Mange har givetvis selv forsøgt at ændre akustikken i deres lytterum, uden egentlig at vide hvad de har lavet. Som udgangspunkt (og evt. slutpunkt) er dette også en glimrende metode, sålænge at ens egne ører fornemmer en forbedring af lydgengivelsen. For dem, der med stor interesse har læst diverse akustiske artikler i High Fidelity og andetsteds, kan der måske være lidt nyt under solen i dette notat.
Eventuelt er der nogle, som har prøvet noget derhjemme, som de vil dele med mig ???
Det er fantastisk svært at gøre rede for hvad der forstås ved, at et rum har en god akustik. Man kan dog nævne parametre, der er med til at give en dårlig akustik, og dermed bør undgås.
-Fokusering af lyd på visse tilhørerpladser.
-Ekkoer (hørbare refleksioner)
-Flutterekkoer (Hørbar serie af periodiske refleksioner)
-Enkelte, svagt dæmpede, hørbare egenfrekvenser.
-Generende baggrundsstøj
Den primære akustiske design faktor, ved stort set alle akustiske forbedringer i rum, er efterklangstiden. Som en grov tommelfingerregel gælder i følge de fleste teorier, at rum beregnet til tale og gengivelse af optaget musik bør være så lav som mulig, da det er den direkte og ikke efterklangen i reproduktionsrummet, man er interesseret i.
Den generelle akustiske kvalitet afhænger dog også af rummets form og størrelse, placeringen af lydgiver og modtager, placering af absorptionsmateriale mm.
Forskellige rum giver de samme højttalere forskellige frekvensresponser i lyttepositionen og lyder dermed også forskelligt. Dette er ofte en overset ting for mange mennesker, som er interesseret i at opnå en optimal lydgengivelse.
Det generelle mål med et rumakustisk projekt er at opnå en akustik i rummet, der er neutral, dvs. rummet må ikke farve den i rummet udsendte lyd på nogen måder.
Farvningen af lydgengivelsen i et rum afhænger bl.a. af kilde og lydmodtagers position, frekvensindhold af lydkilde, antallet af egensvingninger der anslås, efterklangstiden og den indbyrdes frekvensafstand mellem de anslåede egenfrekvenser. Herved kan kompleksiteten ses, da al musik har et frekvensindhold der varierer, og derved anslår forskellige egenfrekvenser.
Hvis der opnås en akustik, som er neutral, vil lydgengivelsen i rummet ikke give forskellige audioprodukter (eks. højttalere) lydmæssige fordele frem for andre produkter.
Med andre ord er akustikken i et rum en uhyre kompleks størrelse, der er meget svær at forholde sig objektivt til.
Før dimensioneringen af et lytterum, bør der opnås et kendskab til teorien......man bygger jo heller ikke en forstærker uden at kende Ohm's lov. Teorien er her tilpasset den aktuelle situation, dvs. lydgengivelse i små / mellemstore lukkede rum.
Den teori, der på nuværende tidspunkt er tilstede indenfor akustikens verden, består som oftest af matematiske udtryk, som alle er baseret på tilnærmelser og forsøg, der ikke direkte kan overføres til praksis, bl.a. pga. kompleksiteten i den virkelige verden. Dette faktum er jo også gældende for højttalerkonstruktioner mm., men ønsker man at formidle viden er teori, matematiske formler mm., som oftest den mest anvendte fremgangsmetode. De fleste vil jo nok også give mig ret i, at teori er god, men erfaring er bedre.
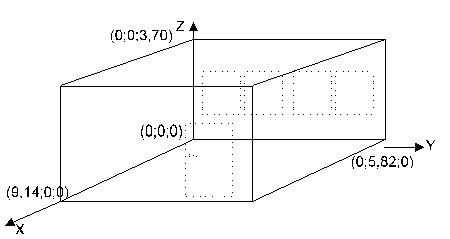
Ved den efterfølgende "teorigennemgang" er der som beregningseksempel anvendt et rum med følgende dimensioner :

Figur 1 : Rumdimensioner, i meter, for rumeksemplet.
Dette rum er nok noget større end det de fleste af os har som dagligstue, men beregningerne kunne lige såvel være gennemført med et mindre rum.
2.1 Absorption
Når en lydbølge, der udbreder sig i luft, rammer et materiale, f.eks. en væg, vil en del af lydeffekten reflekteres, en del absorberes og en del transmitteres, således at der udstråles lydeffekt på den anden side af materialet. Et materiales evne til at absorbere lyd karakteriseres gennem absorptionskoefficienten a (alfa), der er defineret som forholdet mellem den lydeffekt, der absorberes og transmitteres af materialet, og den mod materialet indfaldende effekt. Absorptionskoefficienten for et givet materiale er som regel stærkt afhængig af frekvensen af den indfaldende lyd.
Man skelner i praksis mellem 3 typer af passive absorbenter :
Porøsitetsabsorbenter: eksempelvis Rockwool, glasuld mm. har en god absorptionsevne inden for et bredt frekvensområde afhængigt af materialets tykkelse og placering. Absorptionsevnen vokser med frekvensen, og porøsitetsabsorbenter finder derfor først og fremmest anvendelse, hvor absorption ønskes ved middelhøje og høje frekvenser. Porøsitetsabsorbenter virker ved det energiforbrug, som opstår ved luftpartiklernes bevægelse inden i det porøse materiale. Herved omdannes luftpartiklernes bevægelsesenergi ved friktion til varmeenergi. For at opnå stor friktion skal materialet have et stort antal små åbninger eller porer, så der skabes en stor gnidningsmodstand for lydtrykbølgerne.
For porøsitetsabsorbenter er det karakteristisk, at der opnås en forøget absorption ved lave frekvenser ved at trække absorbenten et stykke, d, ud fra en bagvedliggende flade
Jvf. teorien kan absorptionskoefficienten, for en porøs absorbent, skrives som :

Formel 1
Hvor f er frekvensen (som varierer), h er tykkelsen af det porøse materiale (her =0,02m), r er massenfylden af luft (=1,2 kg/m3), c er lydhastigheden (=344m/s), F Fibral er den specifikke strømningsmodstand for det valgte materiale (her Rockfon Fibral ; = 30000 N× s/m4) og d er materialets afstand til en begrænsende flade. Det bør bemærkes, at der er absorptionsmaxima for d = l /4+n× l /2 hvor n=0,1,2,3....osv.
På figur 2 er formel 1 plottet. Figur 2 viser absorptionskoefficienten a , for en porøs absorbent trukket ud i forskellige afstande fra en væg.

Figur 2 : Plot af absorptionskoefficienten for et porøst materiale i hhv. 0,7m og 1m foran en hård væg.
På figur 3 ses en illustrativ skitse af et porøst lags mest gunstige placering foran en hård væg :

Figur 3 : Skitse af gunstig placering af porøst materiale foran en hård flade. Den indfaldende lydbølges hastighedsprofil er ligeledes skitseret for vinkelret lydindfald mod den hårde flade.
Resonatorabsobenter & 3. Membranabsorbenter : Absorption ved lave, middelhøje frekvenser eller i et afgrænset frekvensområde kan frembringes ved hjælp af resonator- og membranabsorbenter. Disse giver kun absorption inden for et snævert frekvensinterval, der dog kan udvides ved - i forbindelse med resonator- eller membranabsorbenten - at anvende en porøsitetsabsorbent. Eksempler gives ikke her.
Efterklangstid (T) er defineret som den tid, der går fra en lydkilde i et rum afbrydes, til lydtrykket er faldet 60 dB. På grund af maskeringsfænomener (se figur 4) bør T i rum til lydgengivelse være lav. Endvidere gælder at jo kortere T er i et givet rum, desto større klarhed opnås.

Figur 4 : Maskeringseffekt af smalt støjbånd.
På figuren ses, at menneskets tærskelkurve for lydopfattelse ændres ved udsættelse for et smalt støjbånd. Dvs. ved lydgengivelse i rum med lang T vil lydtrykniveauet forblive højt i lang tid og dermed maskere nye lydsignaler, en uønsket effekt, der kan elimineres ved nedsættelse af T.
T må dog heller ikke være for lav, da menneskets rumillusion ved lydgengivelse er nært knyttet til tidlige refleksioner, hvilket naturligvis ikke kan opnås i et lyddødt rum.
Den mest kendte formel til beregning af efterklangstiden i et rum er Sabines formel :
![]()
Formel 2
Hvor V er rummets volumen, c er lydens hastighed i luft (» 344 m/s, se senere), A er absorptionsmængden i rummet givet ved :
![]()
Formel 3
Hvor Si er arealet af overflade nr. i med absorptionskoefficienten a i , nj er antallet af enheder (fx. personer) der hver har absorptionsarealet Aj , m er luftabsorptionen pr. meter (se tabel 1) og V er igen rummets volumen. Tegnet S betyder summationen af de efterfølgende elementer : Sgulv× a gulv + Sloft × a loft .....
Sabines formel er god til en hurtig til en estimation af T i et givet rum, men giver desværre kun troværdige resultater når man regner på hårde rum (dvs. lang T).
Derfor fandt kloge hoveder på følgende udtryk :

Formel 4
Som kaldes Eyrings formel, navngivet efter "opfinderen". Symbolerne har samme betydning som i formel 2, Ln er funktionen den naturlige logaritme. For at formel 2 og 4 kan bruges til noget i praksis skal man kende absorptionskoefficienten a for de materialer som der normalt findes i en stue, se tabel 2.
Centerfrekvens af 1/1 Oktav bånd [Hz] |
Dæmpningskoefficient, m, for luft [1/m] |
| 125 | 0,0000 |
| 250 | 0,0000 |
| 500 | 0,0004 |
| 1000 | 0,0010 |
| 2000 | 0,0024 |
| 4000 | 0,0061 |
Tabel 1 : Dæmpningskoefficient, m, for luft [1/m]
Centerfrekvens af 1/1 oktav bånd [Hz] |
||||||
Materiale |
125 |
250 |
500 |
1000 |
2000 |
4000 |
Åbning til det fri (per definition) |
1 |
1 |
1 |
1 |
1 |
1 |
Gardiner (0.2 kg/m2) hængt 90 mm fra væg. |
0,05 |
0,06 |
0,39 |
0,63 |
0,7 |
0,73 |
Glat puds på mursten eller beton. |
0,01 |
0,01 |
0,02 |
0,02 |
0,02 |
0,04 |
Upudset teglstensvæg |
0,02 |
0,03 |
0,03 |
0,04 |
0,05 |
0,07 |
Solid trædør |
0,14 |
0,1 |
0,06 |
0,08 |
0,1 |
0,1 |
Tæppe, 5 mm tykt (gennemsnit af typer) |
0,05 |
0,05 |
0,20 |
0,30 |
0,50 |
0,55 |
Ca. 3 mm linoleum eller vinyl på beton |
0,02 |
0,03 |
0,04 |
0,05 |
0,05 |
0,01 |
Person på polstret stol.....del af gulvareal 0,90m × 0,55m |
0,55 |
0,86 |
0,83 |
0,87 |
0,90 |
0,87 |
Tabel 2 : Absorptionskoefficienter(a ) for forskellige typer materialer.
Når T ønskes beregnet skal man altså bestemme voluminet af rummet, overfladearealerne af materialerne henført til overfladerne i rummet, samt hvad de består af. Herefter skal, man eksempelvis for hvert 1/1 oktavbånd fra 125Hz til 4000Hz, finde materialernes absorptionskoefficienter. Man er nu klar til indsætte værdierne i enten formel 2 eller formel 4.
Endvidere mener mange, at efterklangstiden bør være så ensartet som muligt i alle oktavbånd således, at alle frekvenser behandles ens. Som det ses ud fra absorptionskoefficienterne i tabel 2, er det ofte svært at få efterklangstiden ved de lave frekvenser ned. Men som en tommelfingerregel vil en placering af en stor porøs absorbent i hjørnerne af rummet kunne hjælpe en del på dette problem, idet der er trykmaksimum for alle frekvenser i hjørnerne af et rektangulært rum. Dette vil dog også sænke efterklangstiden ved de andre frekvenser. Hermed ses, at det kan være en kompliceret proces at optimere et rums efterklangstid.
En af de væsentligste årsager til, at lydgivere lyder forskelligt dels i forskellige rum og dels i forskellige positioner kan forklares vha. bølgeteorien i lukkede rum. Når bølgeteorien indføres, betragtes et rum som en kompleks resonator, der har mange vibrations svingningstyper, hver med sin karakteristiske egenfrekvens. Sættes en lydgiver ind i et rum, opbygges bl.a. axiale stående bølger ved en mængde frekvenser, de såkaldte karakteristiske egenfrekvenser for rummet.
Det totale antal egenfrekvenser er, for et tomt rektangulært rum med plane, parallelle og fuldstændigt reflekterende overflader, givet ved følgende udtryk :

Formel 5
Hvor C, lydens hastighed, er givet ved

Formel 6

Hvilket ved indsættelse i formel 6 ved 20° celsius giver :
![]()
Variablerne i, ,j og k i formel 5 er alle heltallige (= 0,1,2,3,...) og kaldes bølgeindekser, som beskriver hvilke egenfrekvenser, der betragtes. Man opdeler svingningstyperne, der kan forekomme i et rum, i 3 typer.
| Axiale svingninger (i): 1 dimensionale, to af indekserne (i,j,k) er 0. Det er disse svingningstyper, der forårsager flutterekkoer. | Tangentielle svingninger (j) : Bølgekomponenterne er tangenter til ét par af rummets overflader og reflekteres af to andre par. Dvs. 2 dimensionale. | Oblique svingninger (k): Bølgekomponenterne er skrå og rammer derfor alle rummets 6 overflader. Dvs. de er 3 di-mensionale. |
På figur 5 er de tre svingningstyper illustreret.

Ifølge teori, har en aksial svingning et energiindhold på 3 dB mere end en tangential svingning og 6 dB mere end en oblique svingning. Udfra dette har man konkluderet, at de aksiale svingninger er de svingningstyper, der har størst sandsynlighed for at blive individuelt hørbare/betydende. Undtagelsen for dette er, hvis enkelte af de tangentielle eller oblique svingninger ligger alene i et stort frekvensområde.
For at få en fornemmelse af hvordan formel 5 fungerer indsættes rumdimensionerne :
Højde = 3,70m, Bredde = 5,82m og Længde = 9,14m i formel 5 og tabellægges for de laveste frekvenser :
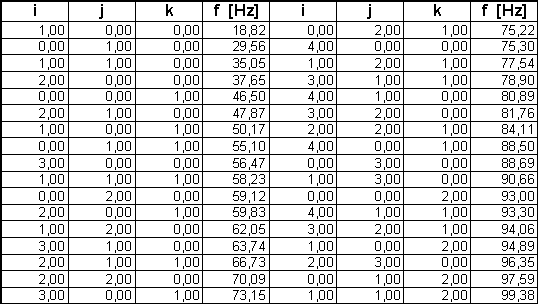
Tabel 3 : Rumeksemplets beregnede egenfrekvenser under 100 Hz.
I tabel 3 ses, at for de laveste frekvenser er den indbyrdes afstand mellem egenfrekvenserne størst, og for stigende frekvenser stiger antallet pr. frekvensinterval. Generelt gælder, at hvis egenfrekvenserne ligger grupperet om få frekvenser, er dette dårligt for akustikken pga., at lydtryksniveauet hæves ekstra kraftigt ved en exitering af rummet ved disse frekvenser. Udfra tabel 3ses, at dette eventuelt er et problem i det rumeksemplet ved ca. 47Hz, 57 Hz, 63Hz, 75 Hz, 81Hz, 89Hz, 94 Hz og 98Hz.
Hvis rummet exciteres med en af disse lave egenfrekvenser vil lydgengivelsen i rummet forstærkes og subjektivt høres dette som en "boom" lyd. Det er derfor ønskeligt at dæmpe specielt disse frekvenser i ethvert lytterum, såfremt det konstateres, at de er meget fremtrædende i rummet.
Ved medium og høje frekvenser ændrer selv alvorlige kamfiltereffekter, stammende fra stående bølgeinterferenser, ikke den modtagede spektrale balance, og medfører heller ikke en hørbar farvning af lyden. Dette skyldes, at tætheden af rummets egenfrekvenser vokser ved stigende frekvenser. Problemerne er dog anderledes ved lave frekvenser, som illustreret ovenfor, derfor behandles dette emne nærmere :
Studier af ovenstående fænomen konkluderer, at lytter og lydgiver ikke bør placeres i lydtryksminima fra stående bølger (axiale svingninger) , stammende fra rummets laveste egenfrekvenser. Dette skyldes de store lydtryksændringer, der forekommer, ved blot få centimeters flytning fra minimaet, lydtryksændringerne er væsentligt mindre ved maxima. Placeringen af disse minima ved lave frekvenser er, jvf. ovenstående, interessante at få kortlagt ved et ønske om en optimal lytter og højttalerplacering. (Se figur 6 & 7) Endvidere konkluderes, at placeringsfølsomheden aftager når højttaleren placeres væk fra de nærmeste vægge......dette må være kendt af de fleste.
Anbringes højttaleren eksempelvis i et trykmaximum for en given lav egenfrekvens vil denne blive kraftigt fremhævet af højttaleren og kraftigt dæmpet ved et trykminimum. For højere frekvenser ligger de stående bølger så tæt, at trykforskellene udligner hinanden.
På figur 6 & 7 er placeringen af de laveste axiale frekvensers lydtryksminima i rummet vist. Her ses en tendens til at antallet af egenfrekvensernes lydtryksminima stiger jo tættere man kommer på de begrænsende flader. Dette relateres til praksis ved at sikre, at lytte-/højttalerposition fjernes fra vægge. (velkendt)

Figur 6 : Beregnede minimum lydtrykspunkter for de laveste axiale svingninger (Rummet set i længde/bredde planet oppefra)
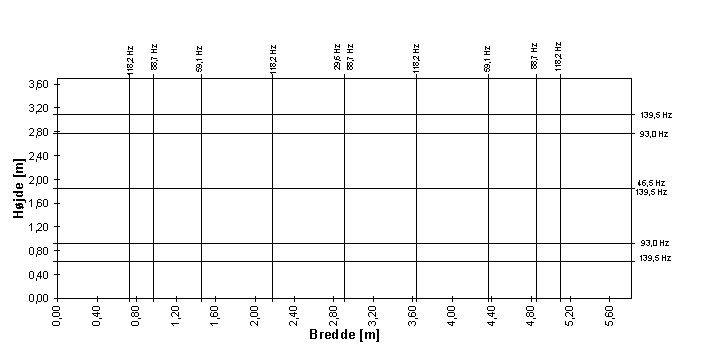
Figur 7 : Beregnede minimums lydtrykspunkter for de laveste aksiale svingninger (Rummet set i bredde/højde planet)
Figur 6 & 7 er fremkommet ved at betragte de laveste aksiale svingninger for de 3 par modstående flader i rummet, og for hver af svingningerne beregne afstandene svarende til :
l /4 + n· l /2 meter , hvor n =0,1,2,3,.... (Se figur 8) .

Figur 8 : Aksial svingning. På figuren ses en stående bølge mellem to bøjningsstive vægge, med tilhørende lydtrykskurve som fkt. af afstanden.
4. Forudsætninger for statistisk rumakustik
For at sikre anvendelsen af statistisk rumakustik (fx. anvendelse af Sabines formel) skal lydfeltet der måles i / regnes på, være diffust. Lydfeltet i et givet rum kan regnes for diffust for frekvenser over Schröders grænsefrekvens fg :
![]()
Formel 7
T= 0,3s er her sat som den ønskede efterklangstid i rummet. Bemærk at voluminet, der benyttes, er for en højde af rummet på 3,7 m. Udfra formel 7 kan lydfeltet ikke regnes for diffust for frekvenser under 78 Hz. For T > 0,3s er fg endnu større pga. den længere efterklangstid.
5. Overvejelser vedr. placering af lytter
For at opnå, at man som lytter sidder i det direkte lydfelt og ikke det reflekterede bør lyttepositionen placeres hensigtmæssigt. Dette kan i praksis realiseres vha. nogle af de nedenstående overvejelser.
Hvis indflydelsen af det direkte lydfelt skal være stor, hvilket er ønskværdigt da det er rummets svar på påvirkninger, som til en vis grad er uinteressante. Ønskes dette, er det nødvendigt, at man ikke sætter sig længere væk fra højttalerne end afstanden svarende til den dobbelte halradius. Halradius er givet ved :
![]()
Formel 8
V er rummets volumen, p » 3,141, T er efterklangstiden og Q er en punktlydkildes (endnu en tilnærmelse) retningsfaktor : Q = 1 for fri placering, Q = 2 ved væg, Q = 4 ved kant og Q = 8 i hjørne. For Q = 1 og Q = 8 fås :
![]()
Dvs. ved placering af lydgiver i et hjørne, bør lyttepositionen placeres i en afstand på mindre end 7,5 meter fra lydgiveren under forudsætning af, at den ønskede efterklangstid på 0,3 sek. er realiseret. Endvidere ses der udfra formel 8 at jo længere T er, desto tættere skal man på lydkilden for at størstedelen af lydenergien kommer fra det direkte lydfelt.
Langt de fleste højttalere er ikke rundtstrålende punktkilder, men udstråler som oftest langt mere lydenergi i fremadretningen end bagud. Dette faktum er med til gøre kravet til afstanden fra højttalere til lytteposition mindre.
Ved målinger i rum er det også almindelig praksis ikke at vælge målepunkter, som ligger tættere end l /4 fra rummets begrænsningsflader, hvor l er bølgelængden af den laveste frekvens, der indgår i målingen .
Eksempel : Ønskes den laveste frekvens, der skal indgå i målingerne, sat til 50 Hz bør mikrofonen anbringes minimum :
![]()
Formel 9
fra rummets begrænsningsflader.
6. Flutterekko, ekko & refleksioner
Flutterekkoer og ekkoer er uønskede og generende effekter.
Flutterekkoer optræder når både lydkilde og modtager befinder sig mellem 2 parallelle hårde overflader, og når andre overflader i nærheden er meget lidt absorberende. Lyd udsendt fra lydgiveren vil have tilbøjelighed til at blive "fanget" mellem de to reflekterende flader og vil oscillere frem og tilbage mellem dem. Lydtrykniveauet vil, pga. den manglende absorption, aftage meget langsomt.
Ekkoer optræder når en kraftig refleksion af en original puls opfattes som en selvstændig puls af en lytter, efter et tidsinterval på ca. 50 msek. Øret fungerer på en sådan måde, at hvis intervallet er under de ca. 50 msek opfattes lyden ikke som et separat ekko, men gør i stedet den opfattede lyd kraftigere.
Ved en lydhastighed på c = 344 m/s svarer 50 mS til en udbredelsesafstand af lyden på :
x = c× t = 344× 50× 10-3 = 17,2 m.
Hermed ses bl.a. hvorledes et givet rum kan "farve" lydgengivelsen, da der i dette tidsrum kan komme refleksioner fra mange flader såfremt rummet er "lille". Begge effekter opfattes subjektivt, og afhænger 100% af det pågældende rum.
Refleksioner fra et rums begrænsningsflader er med til at give tilhøreren en fornemmelse af rum.
Haas effekten blev omtalt tidligere, men hvad er den psykiske virkning af de signaler, der er forsinket mere eller mindre end de ca. 50 ms. i forhold til det oprindelige signal ??
Forskere har udført store forskningsopgaver indenfor den psykoakustiske opfattelse af refleksioner. På figur 9 ses nogle af de resultater, de har opnået.

Figur 9 : Absolutte tærskelkurver for en enkelt lateral (fra siden) refleksion af et talesignal optaget i et lyddødt rum, sammenholdt med en direkte lyd, gengivet under lyddøde forhold. (Den laterale refleksion blev simuleret med en højttaler) På figuren ses at refleksioner, der har delay og niveauer, som ligger under kurve A, ikke høres. Refleksioner, der har delay og niveauer, som ligger over kurve C, opfattes som ekkoer. Det interessante område er mellem kurve A & C, hvor lyden, afhængig af delay og niveau, opfattes som enten rumlig (som i et "rigtigt" rum) eller som en bevægelse af lydkildens position.
Det er vist, at refleksionernes retning har den samme betydning som de laterale, bortset fra de refleksioner der kommer fra den samme retning, som den direkte lyd. Disse refleksioner har en tendens til at blive maskeret med 5-10 dB af den direkte lyd. Skal man tage den yderste konsekvens af dette resultat ses, at der ikke er særlig grund til at opsætte dæmpemateriale lige bagved højttalerne i lytterummet.
Resultaterne vist på figur 9, kan overføres til et lytterum, da det er muligt at ændre fornemmelsen af rum ved at justere mængden af absorptionsmateriale på de flader, der giver de laterale refleksioner.
Udfra ovenstående vil en mulig anbringelse af absorptionsmateriale være således, at de betydende refleksioner for den rumlige fornemmelse begrænses til de laterale. Dvs. en løsning kunne være at anbringe dæmpemateriale i loft og på gulv, svarende til de steder, hvor de tidligste refleksioner fremkommer. Herved er det muligt at justere den rumlige fornemmelse af lydgengivelsen, ved at anbringe mere eller mindre dæmpende/reflekterende materiale på sidevæggene svarende til de laterale refleksioner.
I praksis kan man fra sin lytteposition, ved midlertidigt at påsætte små spejle på væg/loft, finde de steder hvor højttalerne er synlige, her placeres absorptionsmaterialet. Uden måleinstrumenter bruges ørerne, til justere mængden og placeringen.
Uønsket lyd kan betragtes som støj. Det kunne være aktiviteter i tilstødende lokaler, trafik på gangarealer, støj fra ventilationsanlæg og trafikstøj.
Jævnfør figur 4 kan et uønsket støjsignal maskere et ønsket signal, såfremt det er kraftigt nok. Ved at sænke efterklangstiden, dvs. forøge absorptionen, dæmpes et tilstedeværende baggrundsstøjniveau ligeledes. Dette skyldes bl.a. færre tidlige refleksioner (Haas effekten).
Generelt gælder, at en halvering af efterklangstiden betyder, at det generelle støjniveau reduceres med 3 dB, hvilket subjektivt opfattes som en stor forbedring. Denne sænkning af RT vil ligeledes gøre det lettere at retningsbestemme støjen, hvilket ligeledes mindsker generne.
Herudover kan selve årsagen til støjen enten fjernes eller dæmpes lokalt. Et af problemerne med støjbestemmelse er, at mange støjsignaler hverken er stationære i amplitude eller periodiske, hvormed de opnåede resultater vil variere voldsomt mht. tiden. Dette problem kan umiddelbart ikke løses.
Et lytterums hovedfunktion er at reproducere musik via et stereoanlæg, dvs. rummet kan sammenlignes med et radiostudie eller des lige. Ifølge en standard for hvor kraftigt et støjniveau må være i et studie gælder følgende, se figur 10 og 11.

Figur 10 : Noise criteria kurver (NC )for forskellige omgivelser
*Omtrent 65 dBSPL svarer til gennemsnitsværdien for mandlig flydende tale.
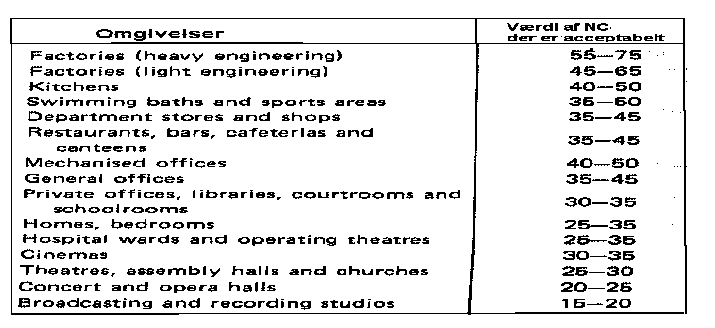
Figur 11: Anbefalede NC værdier for forskellige omgivelser
Værdierne på figur 10 og 11 skal opfattes som en gennemsnitlig acceptabel værdi af støjens niveau, som " fkt. af rummets anvendelse ". Dvs. målet er at få støjniveauet i et lytterum ned på et niveau svarende til værdierne for NC-15 & NC-20 kurverne, værdier herunder er naturligvis ikke at foragte.
8. Den omtrentlige placering af hi-fi udstyret
Da det ved lytning på hi-fi udstyr, er svaret fra højttalerne, og ikke rummet, der er det primære ønske, bør lytter og højttalere være placeret således, at frekvenskarakteristikken på lyttepositionen bliver så lineær som muligt. Denne optimale placering kan, rent måleteknisk, ikke findes, før rummet har den ønskede efterklangstid (T) og de relevante højttalere er tilstede.
I praksis findes frekvenskarakteristikken ved at påtrykke de aktuelle højttalere lyserød støj og i lyttepositionen måle lydtrykket som fkt. af frekvensen. Ved at rykke på højttaler- og lytteposition kan den mest lineære kombination findes.
Før målingerne påbegyndes vurderes en teoretisk optimal højttaler- og mikrofonplacering og denne bruges som udgangspunkt for optimeringen. Jævnfør afsnittene "Bølgeteori i lukkede rum" og "Overvejelser vedr. placering af lytter", er de teoretisk egnede placeringer af lytte- og højttaler-positioner skitseret på figur 12 & 13.

Figur 12 : Teoretisk egnede placeringer af lytte- og højttalerposition. Bredde-længde plan. Linjerne indikerer hvor trykminimum er tilstede for de laveste aksiale egenfrekvenser.

Figur 13 : Teoretisk egnede placeringer af lytte- og højttalerposition. Højde- bredde plan.Linjerne indikerer hvor trykminimum er tilstede for de laveste aksiale egenfrekvenser.
Det bør bemærkes at figur 12 og 13 er en smule misvisende, da man ifølge afsnittet "Bølgeteori i lukkede rum", ikke bør placere lytte- og højttalerposition i lydtryksminima. På figurerne ses, at det er gjort alligevel fordi det forventes at positioner væk fra lydtryksminima, ikke er realisable pga. et ønske om symmetri omkring længderetningen i rummet. Dette skyldes den betagtning at hver højttaler og hvert ører bør "se ind i" den samme akustiske impedans.
Ifølge en international standard beskrives hvorledes den optimale lytteposition bør
være placeret i forhold til lydgiverne, samt hvilke tolerancer, der er acceptable for
frekvenskarakteristikken. Se figur 14 og 15.

| Figur 14 : Reference højttalerarrangement og anbefalede lyttepositioner | Figur 15 : Tolerancegrænser for frekvenskarakteristikken i et rum. Lm er gennemsnitsværdien af niveauet i dB SPL. EBU & ITU er to radio/tv organisationers anbefalede værdier. |
Med ref. til figur 14 anbefales : 2,0m £ B £ 4,0m, samt at D = lytteafstanden (ikke vist på figuren) ligger i niveauet : D = (0,9 ± 0,2)× B. Af andre interessante anbefalede værdier kan nævnes : Afstand af højttalere fra vægge ³ 1m.
Ovenstående er kun retningslinier, og de fleste hi-fi entusiaster bruger deres ører som det vigtigste redskab i denne proces.
Skrevet af :
Johnny Andersen
9. Velegnet litteratur for vidensøgende personer
Nr: |
Titel |
Forfatter |
Udgivelsesår / Udgave |
Specielt sidenr : |
1 |
Architectural Acoustics | K.B. Ginn (Brüel & Kjær) | 1978 / 2. |
|
2 |
Sound waves in rooms | P.M. Morse & R.H.Bolt | Reviews of mod-ern physics, April 1944,Vol16,No.2 |
69-150 |
3 |
The acoustic design of talk studios and listening rooms | C.L.S. Gilford | AES Journal Vol. 27 No.1/2 1979 |
17-31 |
4 |
Lydreflektion og -absorption | Jens Holger Rindel | 1981 (1990) |
10-14 |
5 |
The distribution of the low frequency sound field and its relation to room equalization | Jan Abildgaard Ped-ersen, Kjeld Herman-sen & Per Rubak | Preprint fra AES 96. forsamling februar 1994 |
|
6 |
Stationære lydfelter i rum | Jens Holger Rindel | 1981 |
|
7 |
The detection of reflections in typical rooms. | S. Olive & F. E. Toole | AES Journal Vol. 37 No. 7/8 1989 |
539-553 |
8 |
Rumakustisk måleteknik. Note til kursus 5142 på DTU | Anders Christian Gade | 1988 |
|
9 |
Anvendt rumakustik, Note til kursus 5142 på DTU | Jens Holger Rindel | 1984 /2. |
|
10 |
Lydabsorbenter (Notat R) Note til kursus 5142 på DTU | Jens Holger Rindel | Nov. 1982 |
|
11 |
Rumakustik : SBI anvisning 137 | Statens byggeforskningsinstitut | 1984 |
Litteraturen skrevet af Jens Holger Rindel og Anders Christian Gade er tilgængelig på DTU, nærmere betegnet på Institut for Akustisk teknologi, bygning 352.